在平面几何中,我们常常会碰到与路径相关的问题,主要有三种表现形式:第一,对于给定的平面几何图形,如果已知起点和终点,按照指定的规则,求不同路径的数量;第二,对于给定的平面几何图形,要求走完每一段路,求最短路径;第三,计算平面图形中两点之间的最短距离。前期我们已经详细介绍过第一种情形,本次重点介绍第二种。
▼▼考前行测申论冲刺资料-扫码领取▼▼

在讲解题方法前,我们先铺垫一些基础概念:
第一,对于平面图形上的任何一点,如果从这一点出发的线段有奇数条,则这个点被称为“奇点”,这是“一笔画”中最基本的概念。不存在有奇数个“奇点”的图形。
第二,没有“奇点”(0个奇点)的图形可以一笔画出;有2个“奇点”的图形,也可以一笔画出。
奇点个数为0或者2时,图形可以一笔画出,区别在于:
当奇点个数为0时,对起点没有要求,可以从任意一点回到另一点;
当奇点个数为2时,只能从一个奇点回到另一个奇点。
第三,有4个及4个以上“奇点”的图形,不能一笔画出,有2N个奇点,则需要N笔才能画出。
有了上述基础知识后,我们来讲最短路径类题型。
对于给定的平面几何图形,要求走完每一段路,求最短路径,解题方法为:
1.确定奇点的个数
2.(1)当未指定出发点时,通过连接图形中已有的线段(所连线段要最短),将奇点的个数变为2个。
(2)当指定起点为偶点时,通过连接已有的线段(所连线段要最短),将奇点的个数变为0个。
3.计算原图形中的所有线段的总长度与连接线段长度之和即为所求的最短路径。
理论比较抽象,我们通过几道例题一起来看一下:
【例1】某公园的道路由如图所示的5个正六边形组成,每个六边形每条边的长度都是100米,保安员从道路上某一点出发巡视完所有的道路至少要走多少米?
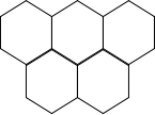
A.2600 B.2800
C.3000 D.2300
【答案】A
【解析】第一步,本题考查几何问题,属于最短路径类。
第二步,该图共有23条线段、8个奇点,题中未指定出发点,故至少要画8÷2=4笔完成该图,可知走完所有道路至少要重复3条边。
第三步,由于每一段都是100米,所以至少走(23+3)×100=2600米。
因此,选择A选项。
【例2】一块由两个正三角形拼成的菱形土地ABCD周长为800米,土地周围和中间的道路如图所示,其中DE、BF分别与AB和CD垂直。如要从该土地上任何一点出发走完每一段道路,问需要行进的距离最少是多少米?
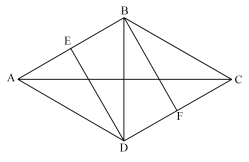
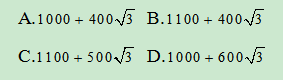
【答案】B
【解析】第一步,本题考查几何问题,属于最短路径类。
第二步,图中共有A、E、F、C四个奇点,题中未指定出发点,故至少要画4÷2=2笔完成该图,说明必有重复路段。要求行进的距离最少,则需重复路径最少,可连接CF,奇点个数变为2个,重复路段为CF。

因此,选择B选项。
【注意】若忽略重复线段,易误选A。
【例3】某社区道路如下图所示,社区民警早上9点整从A处的办公室出发,以每分钟50米的速度对社区内每一条道路进行巡查(要求完整走过整个社区内的每一段道路),问他最早什么时候能完成任务返回办公室?
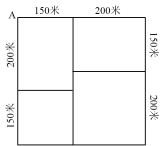
A.9:54 B.9:50
C.9:47 D.10:00
【答案】A
【解析】第一步,本题考查几何问题,属于最短路径类。
第二步,如下图,共有G、H、I、J四个奇点,题中指定从A点(偶点)出发,回到A点,必须使奇点个数为0,要将4个奇点都变成偶点,需要重复2段。要求行进的距离最少,故需重复路径最少,可连接HI和JG,奇点个数变为0个,重复路段为HI和JG。
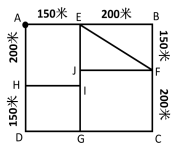
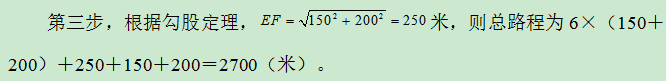
第四步,社区民警完成任务所需的时间为2700÷50=54(分钟),即他最早9:54能完成任务返回办公室。
因此,选择A选项。
对于平面几何中的最短路径类问题,即对于给定一个平面几何图形,要求走完每一段路,求最短路径的题目,有两个核心点,一是数奇点的个数;而是起点有没有指定。如果起点指定为偶点,需将奇点个数变为0,如果未指定,只需将奇点个数变为2即可,由奇点变偶点的方式是连线或者搭桥。当然,需要各位同学把握好题目特征以及具体操作步骤,只有熟练掌握才能灵活运用。











