近几年概率问题考查的越来越多,其中几何概率也随之成为一个小的热点模型。几何概率的本质非常简单,考试题目难度一般不大,如果掌握了几何概率的本质则很容易拿到这部分题目的分数。
先来看定义:如果每个事件发生的概率只与构成该事件区域的长度、面积或体积成比例,则称这样的概率模型为几何概率模型,简称为几何概型。
这个定义的本质其实就是在一个几何维度中,每一个点被取到的机会都一样。相对于基础的概率公式,把可以计数的“满足条件的情况数”变成了不可计数的“满足条件的长度/面积/体积”,将等可能事件的概念从有限向无限进行了延伸,也是初中学习的内容。那么几何概率的式就变成了 。
。
【例1】射击用的靶子是由若干个同心圆组成,最中心的圆代表10环,而10环外圈的一个圆环代表9环。在随机射击时,若要使得击中10环和9环的概率相同,那么10环外圈半径与9环外圈半径的比值为:

【答案】D
【解析】第一步,本题考查几何概率。
第二步,要使得击中10环和9环的概率相同,根据几何概率基本公式,则10环和9环的面积相同。如下图所示,设10环外圈的半径为r1,9环外圈的半径为r2,根据面积相等有πr1²=πr2²-πr1²,整理得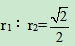

因此,选择D选项。
在圆形区域内考查几何概率比较多见,需要根据圆内各个半径计算面积的比值从而计算概率。2018年上半年多省市联考也考到了这样一道几何概率:
【例2】小波通过往圆圈里投掷米粒(米粒本身长度不计,视为一个点)的方式决定自己的周末活动。经过试验,他将米粒投进圆圈内的成功率达到100%,但投掷在圆内的位置随机。如果米粒到圆心的距离大于圆半径的一半,那么他周末去看电影;若米粒到圆心的距离小于半径的1/4,他会去打篮球;否则,他将在家看书。据此可知小波周末不在家看书的概率为:
A.13/16
B.2/5
C.3/5
D.1/16
【答案】A
【解析】第一步,本题考查几何概率问题。
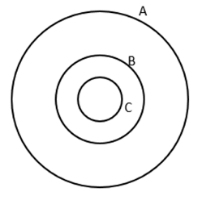
第二步,如下图所示,赋值圆圈A的半径为4,则到圆心距离为圆A半径一半的圆B的半径为2,到圆心距离为圆A半径的1/4的圆C半径为1,根据面积的比等于半径之比的平方,可得圆A、B、C的面积之比为16∶4∶1,那么留在家看书的概率为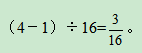 。
。
第三步,小波周末不在家看书的概率为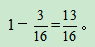
因此,选择A选项。
这两道题都是近两年考查几何概率的考题中比较简单的题目。近几年也考查过一些比较难的题目,这一类题目需要考生理解模型,从而在建造几何模型的过程中胸有成竹。当然如果考场上第一次遇见,没思路也可以放弃。
【例3】将一长度为L的线段任意截成三段,设P1为所截的三线段能构成三角形的概率,P2为所截的三线段不能构成三角形的概率,则下列选项正确的是:
A.P1=P2 B.P1>P2
C.P1<P2 D.不能确定P1、P2的大小关系
【答案】C
【解析】第一步,本题考查几何概率问题。
第二步,如图,设线段长度为1,第一个点坐标为y,第二个点坐标为x,三条线段长度分别为y、x-y、1-x。
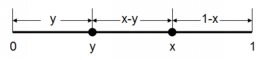
由于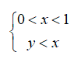 ,因此x、y的取值区间如图:
,因此x、y的取值区间如图:
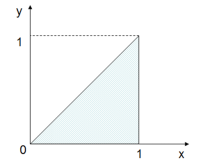
要让三条线段能够组成三角形,则需要两边之和大于第三边,用公式表达:
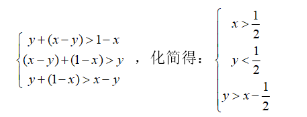
用图形表示:
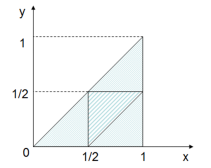
中间阴影部分即为可以构成三角形的x、y取值。
第三步,根据图形面积可知,能够构成三角形的概率P1为1/4,不能构成三角形的概率P2为3/4,则P1<P2。
因此,选择C选项。
本题难度十分大,但这道题在考场上也可以根据选项去选择:一根线段分成3截,两边之和与第三边的关系为:大于、等于或小于。三角形两边之和大于第三边、两边之差小于第三边,所以能构成三角形的概率小于不能构成的概率。
这种在直角坐标系里寻找几何概率的题目在公考中并不少见。无独有偶,2019年江苏考了一道与【例3】几乎一模一样的题目,只是选项更不好猜测。
【例4】将一根绳子任意分成三段,则此三段能构成一个三角形的概率是:
A.1/4 B.1/3
C.1/2 D.3/4
本题答案选择A,做法跟例3一模一样。本题难度很大,华图在线题库后台显示本题正确率只有18%。事实上可以根据选项相关,猜测答案为A、D中较小的那一个。
可以发现,几何概率如果给出了几何模型,就是简单的概率题目,必须拿分;如果需要在直角坐标系中自己构建模型,则可以根据选项猜测正确答案。在考场上不论什么方法,只要能选出正确答案,就是好方法。
更多的考试技巧和考试内容,考生可以扫码购买考前冲刺密卷,试卷包含考试内容预测,每道题解析讲解,能够1:1的还原考场试卷,还有申论人工批改环节,可以更加高效的帮助考生成功上岸!
先来看定义:如果每个事件发生的概率只与构成该事件区域的长度、面积或体积成比例,则称这样的概率模型为几何概率模型,简称为几何概型。
这个定义的本质其实就是在一个几何维度中,每一个点被取到的机会都一样。相对于基础的概率公式,把可以计数的“满足条件的情况数”变成了不可计数的“满足条件的长度/面积/体积”,将等可能事件的概念从有限向无限进行了延伸,也是初中学习的内容。那么几何概率的式就变成了
 。
。【例1】射击用的靶子是由若干个同心圆组成,最中心的圆代表10环,而10环外圈的一个圆环代表9环。在随机射击时,若要使得击中10环和9环的概率相同,那么10环外圈半径与9环外圈半径的比值为:

【答案】D
【解析】第一步,本题考查几何概率。
第二步,要使得击中10环和9环的概率相同,根据几何概率基本公式,则10环和9环的面积相同。如下图所示,设10环外圈的半径为r1,9环外圈的半径为r2,根据面积相等有πr1²=πr2²-πr1²,整理得

因此,选择D选项。
在圆形区域内考查几何概率比较多见,需要根据圆内各个半径计算面积的比值从而计算概率。2018年上半年多省市联考也考到了这样一道几何概率:
【例2】小波通过往圆圈里投掷米粒(米粒本身长度不计,视为一个点)的方式决定自己的周末活动。经过试验,他将米粒投进圆圈内的成功率达到100%,但投掷在圆内的位置随机。如果米粒到圆心的距离大于圆半径的一半,那么他周末去看电影;若米粒到圆心的距离小于半径的1/4,他会去打篮球;否则,他将在家看书。据此可知小波周末不在家看书的概率为:
A.13/16
B.2/5
C.3/5
D.1/16
【答案】A
【解析】第一步,本题考查几何概率问题。
第二步,如下图所示,赋值圆圈A的半径为4,则到圆心距离为圆A半径一半的圆B的半径为2,到圆心距离为圆A半径的1/4的圆C半径为1,根据面积的比等于半径之比的平方,可得圆A、B、C的面积之比为16∶4∶1,那么留在家看书的概率为
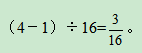 。
。
第三步,小波周末不在家看书的概率为
因此,选择A选项。
这两道题都是近两年考查几何概率的考题中比较简单的题目。近几年也考查过一些比较难的题目,这一类题目需要考生理解模型,从而在建造几何模型的过程中胸有成竹。当然如果考场上第一次遇见,没思路也可以放弃。
【例3】将一长度为L的线段任意截成三段,设P1为所截的三线段能构成三角形的概率,P2为所截的三线段不能构成三角形的概率,则下列选项正确的是:
A.P1=P2 B.P1>P2
C.P1<P2 D.不能确定P1、P2的大小关系
【答案】C
【解析】第一步,本题考查几何概率问题。
第二步,如图,设线段长度为1,第一个点坐标为y,第二个点坐标为x,三条线段长度分别为y、x-y、1-x。
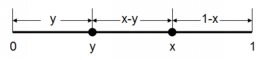
由于
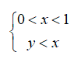 ,因此x、y的取值区间如图:
,因此x、y的取值区间如图:
要让三条线段能够组成三角形,则需要两边之和大于第三边,用公式表达:
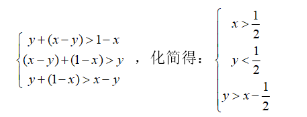
用图形表示:

中间阴影部分即为可以构成三角形的x、y取值。
第三步,根据图形面积可知,能够构成三角形的概率P1为1/4,不能构成三角形的概率P2为3/4,则P1<P2。
因此,选择C选项。
本题难度十分大,但这道题在考场上也可以根据选项去选择:一根线段分成3截,两边之和与第三边的关系为:大于、等于或小于。三角形两边之和大于第三边、两边之差小于第三边,所以能构成三角形的概率小于不能构成的概率。
这种在直角坐标系里寻找几何概率的题目在公考中并不少见。无独有偶,2019年江苏考了一道与【例3】几乎一模一样的题目,只是选项更不好猜测。
【例4】将一根绳子任意分成三段,则此三段能构成一个三角形的概率是:
A.1/4 B.1/3
C.1/2 D.3/4
本题答案选择A,做法跟例3一模一样。本题难度很大,华图在线题库后台显示本题正确率只有18%。事实上可以根据选项相关,猜测答案为A、D中较小的那一个。
可以发现,几何概率如果给出了几何模型,就是简单的概率题目,必须拿分;如果需要在直角坐标系中自己构建模型,则可以根据选项猜测正确答案。在考场上不论什么方法,只要能选出正确答案,就是好方法。
更多的考试技巧和考试内容,考生可以扫码购买考前冲刺密卷,试卷包含考试内容预测,每道题解析讲解,能够1:1的还原考场试卷,还有申论人工批改环节,可以更加高效的帮助考生成功上岸!











