2022年国家公务员报名已经进入到了中后时期，这个阶段报名人数每日都在激增，我们来看看四川巴中市地区的报名情况：2022年国家公务员在巴中市地区招录24个职位，总共28人。截止 10月21日11：00 巴中市地区已经报名772人，其中待审核162人,审核通过610人。整个巴中市地区的国家公务员报考竞争比已经达到了32: 1。下面是具体数据

截止10月21日11：00 ，巴中市地区国家公务员报名数据
地区	职位数	招录人数	报名人数	待审核人数	审核通过	竞争比
四川省	895	1237	40014	6570	33444	44: 1
巴中市	24	28	772	162	610	32: 1

　　根据上表可以看到，截止10月21日11：00 ，全四川已经报名了40014人，其中，巴中市地区报名了772人。另外国家公务员巴中市地区的岗位在整个四川来看是属于报考相对冷门的岗位，因为其竞争比为32: 1小于四川省所有岗位的平均竞争比44: 1。zui后提醒，本次国家公务员报名时间即将于10月24日18:00结束，届时报名入口将自动关闭，各位考生需要尽快在国考报名系统去报名，另外，报名后记得缴费!!

　　国家公务员备考资料>>>>

工程问题在国考中属于常考知识点，在近5年国考中，每年会考到，因此，我们还是应该对此知识点多做练习。对于工程问题主要分为三大类：给定时间型、给定效率型、条件综合型。今天我们主要就给定效率型给大家做以介绍。

题型识别

题干中可以直接或间接找到不同主体之间的效率比

方法技巧

根据效率比赋效率

根据赋的效率和时间求工作总量

根据已知条件问啥求啥

三、例题精讲

【例1】某单位甲、乙、丙三人负责整理一项档案，他们工作5天完成了1/4，之后甲和乙因其他工作被调离，两天后才返回，期间丙继续整理档案。已知甲、乙、丙三人的工作效率之比为4∶3∶2，则完成这项工作共需要花费( )天。

A.20

B.21

C.22

D.23

【答案】C

【解析】由于题干中直接给出了甲、乙、丙三人的工作效率之比，为给定效率型工程问题。

第*步，赋效率，根据甲、乙、丙三人的工作效率之比为4:3:2，赋甲的效率为4、乙的效率为3、丙的效率为2。

第二步，求总量，根据“甲、乙、丙三人负责整理一项档案，他们工作5天完成了1/4”得 1/4工作总量=(4+3+2)×5，即 1/4 工作总量=9×5，可得工作总量=180。

第三步，问啥求啥，设甲乙返回后三人合作共干了x天，列方程得9×5+2×2+9x=180，解得x=14+ ，即甲乙返回后三人合作15天干完了此工程，所以完成此项工程花费总时间为5+2+15=22(天)。

因此，选择C选项。

【例2】有甲、乙、丙三个工作组，已知乙组2天的工作量与甲、丙共同工作1天的工作量相同。A工程如由甲、乙组共同工作3天，再由乙、丙组共同工作7天，正好完成。如果三组共同完成，需要整7天。B工程如丙组单独完成正好需要10天，问如由甲、乙组共同完成，需要多少天?

A.不到6天

B.6天多

C.7天多

D.超过8天

【答案】C

【解析】由“乙组2天的工作量与甲、丙共同工作1天的工作量相同”得2乙=甲+丙，由“甲、乙组共同工作3天，再由乙、丙组共同工作7天，正好完成。如果三组共同完成，需要整7天”得3(甲+乙)+7(乙+丙)=7(甲+乙+丙)，化简得甲、乙、丙三者效率之间的关系甲：乙：丙=3:4:5，由此判断本题为间接给出效率比型工程问题。

第*步，赋效率，根据甲:乙:丙=3:4:5赋甲的效率为3，乙的效率为4，丙的效率为5。

第二步，求总量，B工程总量=10丙=10×5=50。

第三步，问啥求啥，甲、乙共同完成时间=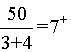，即需要7天多完成。

因此，选择C选项。

四、小结

对于给定效率型工程问题做题时要注意直接给出效率比还是间接给出，直接给出好判断，间接给出需要根据已知条件进行判断，看是否可推出效率之间的关系。