对近年四川省考梳理分析发现,四川省考对几何问题特别青睐,近3年共6次考试中,每一次都会出现几何问题的身影。几何问题对考生而言,既感到很熟悉,熟悉是因为日常生活中都会有所涉及,但更多的只是停留在表象之上,所以考生们对几何问题又特别的陌生,对公式的不熟悉,对几何性质的不敏感,导致做题过程中不知道灵活变通,很难拿到相应的分数,导致考生对几何问题敬而远之。为解考生之忧虑,通过对历年的分析和研究,我们发现几何问题主要考查的是两个方向,其一是几何计算,其二是几何特性。那么今天主要为大家介绍利用几何特性中的尺度扩大理论快速解题,实现效率与正确率的双提升。具体分析如下:
三角形相似是初中几何的重要组成部分,因此,绝大多数考生对于相似并不陌生,稍微复习一下就可以理解三角形相似。如果两个三角形相似,那么对应角相等,对应边成比例。由三角形相似,我们可以推广到二维、三维层面上来。如果一个图形扩大N倍,那么周长扩大N倍,面积扩大N2倍,体积扩大N3倍。这就是尺度扩大理论,我认为要理解尺度扩大理论,只需要把三角形相似原理推广到面积和体积层面即可。该理论对于解决某些几何问题简直可以说秒杀。具体请看例1。
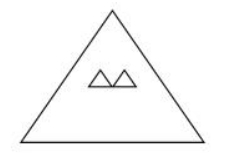
【例1】某演播大厅的地面形状是边长为100米的正三角形,现要用边长为2米的正三角形砖铺满(如图所示)。问,需要用多少块砖?
A. 2763 B. 2500 C. 2340 D. 2300
【解析】这道题目若用常规解法,就需要先算出演播大厅地面的面积,根据其为正三角形且边长为100米,计算出其高为50![]() 米,然后计算出面积为2500
米,然后计算出面积为2500![]() 平方米;然后同理计算出瓷砖的面积为
平方米;然后同理计算出瓷砖的面积为![]() 平方米。需要
平方米。需要![]() 块瓷砖。此题计算过程还好,计算难度不大,但毕竟也要花费不少时间。如果是能想到尺度多大理论,那需要瓷砖的数量就是大正三角形与小正三角形的面积之比,而面积之比又是其边长之比的平方,边长之比是100:2=500:1,那面积之比为2500:1,即需要2500块瓷砖,不用动笔即可口算秒杀出结果。因此选择B选项。该题就是通过尺度扩大理论来快速解题,实现了效率的极大提升,节约了宝贵的时间。
块瓷砖。此题计算过程还好,计算难度不大,但毕竟也要花费不少时间。如果是能想到尺度多大理论,那需要瓷砖的数量就是大正三角形与小正三角形的面积之比,而面积之比又是其边长之比的平方,边长之比是100:2=500:1,那面积之比为2500:1,即需要2500块瓷砖,不用动笔即可口算秒杀出结果。因此选择B选项。该题就是通过尺度扩大理论来快速解题,实现了效率的极大提升,节约了宝贵的时间。
因为例1通过计算也能快速地得到结果,还不能充分体现尺度扩大理论的优势,接下来看看尺度扩大理论在例2中的运用带来的极大好处。
【例2】(2018联考)某甜品店出售一种规则球形的甜品,该甜品由内部中空的球形面皮(每立方厘米成本0.4元)和实心的芝士球(每立方厘米成本1元)组成。无论甜品大小规格如何,其中的芝士球半径始终为甜品半径的四分之三。已知制作半径为1厘米的该甜品成本约为2.73元,那么要制作半径为2厘米的该甜品,成本约为:
A. 5.46元B. 7.45元C. 14.92元D. 21.88元
【解析】该道题目若没有意识到可以使用尺度扩大理论,那么就需要先计算四分之三的芝士球,再求剩下的球形面皮,计算上会有相当大的难度。那么,此题用尺度扩大理论,半径为1厘米和2厘米的该甜品相似比为1:2,那么其体积之比应该为1:8,即半径为2厘米的该甜品的体积是半径为1厘米的8倍,那成本也相应为8倍,计算出结果为21.84元,因此选择D选项。












